评估算法，第一步当然是从数学的角度证明算法的准确性，第二步就要评估算法的效率了。通常会从时间和空间两个角度来评估，作为程序员，掌握基本的算法时间复杂度、空间复杂度的分析方法是很有必要的

什么是算法？

通俗意义上来说，算法就是解决问题的步骤

具有 5 个重要的特征

• 有穷性（必须能在执行有限个步骤之后终止）
• 确切性（每一步骤必须有确切的定义）
• 输入项（有 0 个或多个输入）
• 输出项（有一个或多个输出，没有输出的算法是毫无意义的）
• 可行性（算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步，每一步都可以在限定的时间内完成）

时间复杂度

习惯上将算法语句重复执行的次数作为算法的时间量度（其他很多因素取决于计算机的性能）

用数学概念来描述算法的执行次数，可以把一个算法中语句的执行次数称为语句频度或时间频度，记为 T(n)
当问题规模 n 不断变化时，时间频度 T(n) 也会不断变化
我们需要评估当 n 不断变化时，时间频度 T(n) 的变化规律

若有某个辅助函数 f(n)
当 n 趋向于无穷大时，如果 T(n)/f(n) 的极限为不等于零的常数，则认为 T(n) 与 f(n) 是同量级的函数，记作：T(n) = O(f(n))
O(f(n)) 称为算法的渐进时间复杂度，简称时间复杂度
简单来说，就是 T(n) 在 n 趋于正无穷时最大也就跟 f(n) 差不多大

一般来说，我们并不关心 T(n) 的精确度量，而只是关心其量级

• 保留算法的最高次幂，忽略所有低次幂和高次幂的系数
• 在估算算法的时间复杂度时，均以数据集中最坏的情况来估算

常见的时间复杂度量（由小到大依次）有

• O(1)：常量阶，运行时间为常量
• O(logn)：对数阶，如二分搜索算法
• O(n)：线性阶，如 n 个数内找最大值
• O(nlogn)：对数阶，如快速排序算法
• O(n^2)：平方阶，如选择排序，冒泡排序
• O(n^3)：立方阶，如两个 n 阶矩阵的乘法运算
• O(2^n)：指数阶，如 n 个元素集合的所有子集的算法
• O(n!)：阶乘阶，如 n 个元素全部排列的算法

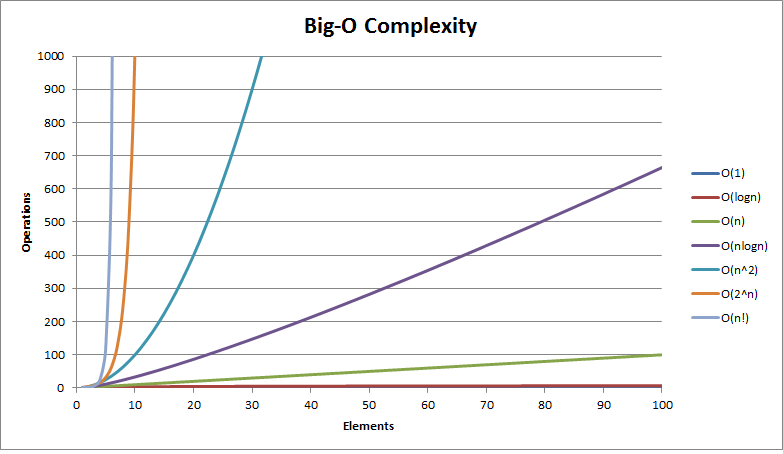
在实时系统中，对系统响应时间要求高，则尽量选用执行时间少的算法

举例

i = 0                           1 次

T(n) = O(1)

a = 0                           1 次
b = 1                           1
for (i = 1; i <= n; i++) {      n+1
    s = a + b                   n
    b = a                       n
    a = s                       n
}

O(1+1+n+1+3n) = O(4+3n)，即 T(n) = O(n)

sum = 0                         1
for (i = 0; i < n; i++) {       n+1
    for (j = 0; j < n; j++) {   n^2
        sum++;                  n^2
    }
}

O(2n^2+n+2)，所以 T(n) = O(n^2)

i = 1
while (i <= n) {
    i = i * 2;
}

设语句 2 的频度是 f(n)，2^f(n) <= n; f(n) <= log2n
取最大值，f(n) = log2n，所以 T(n) = O(log2n)

空间复杂度

一个算法的空间复杂度是指该算法所耗费的存储空间，计算公式计作：S(n) = O(f(n))
其中 n 也为数据的规模，f(n) 在这里指的是 n 所占存储空间的函数

当数据处理量大，而存储空间较少时，则尽量选用节省空间的算法

空间复杂度其实更多的是说一下这个概念
因为当今硬件的存储量级比较大，一般不会为了稍微减少一点儿空间复杂度而大动干戈
更多的是去想怎么优化算法的时间复杂度
所以我们在日常写代码的时候就衍生出了用「空间换时间」的做法，并且成为常态

比如我们在求解斐波那契数列数列的时候我们可以直接用公式去递归求，用哪个求哪个
同样也可以先把很多结果都算出来保存起来，然后用到哪个直接调用
这就是典型的用空间换时间的做法
但是你说这两种具体哪个好，伟大的马克思告诉我们「具体问题具体分析」