Manacher's Algorithm 马拉车算法
2019-04-02
马拉车算法是用来查找一个字符串的最长回文子串的线性方法,是一个叫 Manacher 的人在 1975 年发明的,这个方法的最大贡献是在于将时间复杂度提升到了线性,这是非常了不起的
回文介绍
回文就是正读倒读都一样的字符串,如 “level”, “noon”
求最长回文串,需要遍历去求以每个字符为中心,向两边寻找回文子串
获得最大回文子串的时间复杂度 O(n^2)
而马拉车算法的时间复杂度为 O(n)
马拉车算法
1、预处理
解决奇偶数回文问题)在每一个字符的左右都加上一个特殊字符,如 #
level -> #l#e#v#e#l#
noon -> #n#o#o#n#
处理之后得到的字符串的个数都是奇数个,之前是回文的之后还是回文,不用分情况讨论了
2、求回文子串的半径
处理之后得到的字符串 t
# a # a # b # b # a # b # b # a #
位置 i
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
以 t[i] 字符为中心的回文子串半径数组 p
1 2 3 2 1 2 5 2 1 8 1 2 5 2 1 2 1
怎么计算呢?
如位置 9 的字符是 a,本身算 1,因为 a 字符串本身就是对称的
然后比较 a 左右的字符,相同则 p[9]++,不断向外扩展,最后得到 p[9] = 8
求回文子串的半径有什么用?
以 t[9] = a 为中心的回文是 #a#b#b#a#b#b#a#,原字符串回文 abbabba 长度 7
刚好是 p[9] - 1,即回文子串的半径减 1(#a#b#b#a#b#b#a#)
这是个通用规律,可以思考、去求证下
算法核心介绍
引入两个辅助变量 mx 和 id
mx 是之前计算中最长回文子串的右端点的最大值
id 为取得 mx 的回文中心位置
mx > i
p[2 * id - i] 对称点 j 的回文子串的半径
mx - i 位置 i 到 mx 的距离
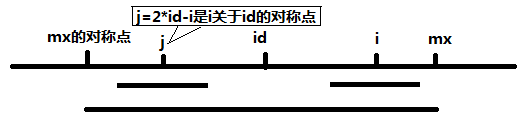
如果 p[2 * id - i] < j - mx' = mx - i
根据对称性,即以 j 为中心的回文包含在以 id 为中心的回文里面
id 到 mx、mx' 左右对称
==> p[i] = p[j] = p[2 * id - i]
mx > i
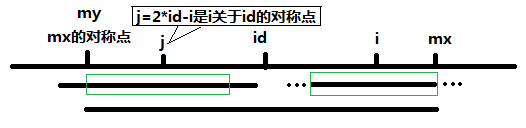
如果 p[2 * id - i] >= j - mx' = mx - i
表示 i 为中心的回文右边界超过了 mx
因为 mx 右侧的字符是未计算的,需要再循环比较
==> p[i] = mx - i
i > mx
无法对 p[i] 做更多的假设,只能 p[i] = 1,然后再去匹配了
算法核心代码
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
具体实现
package main
import (
"bytes"
"fmt"
"strings"
)
func main() {
s := "aabbabba"
fmt.Println(manacher(s))
// abbabba
}
// 马拉车算法
func manacher(s string) string {
char := byte('#')
s = changeStr(s, char)
// 存储以字符 N[i] 为中心的最长回文字串的最右字符到 N[i] 的长度
p := make([]int, len(s))
// mx 之前计算中最长回文子串的右端点的最大值,id 为取得 mx 的回文中心位置
var id, mx int
// 最大回文中心位置
maxCenterIndex := 1
// 去除边界 ^ $
for i := 1; i < len(p) - 1; i++ {
// j 是 i 以 id 为中心的对称点
j := 2 * id - i
// i 处在右边界 mx 的左边
if mx > i {
if mx - i > p[j] { // 对称点 j 的回文串没有越界,根据对称关系赋值
p[i] = p[j]
} else { // 越界,则先赋值 mx - i
p[i] = mx - i
}
}
// 循环比较
for s[i + p[i]] == s[i - p[i]] {
p[i]++
}
// i 的右边界超出 mx
if i + p[i] > mx {
mx = i + p[i]
id = i
}
// 计算最大回文中心位置
if p[i] > p[maxCenterIndex] {
maxCenterIndex = i
}
}
// 最大回文串长度
//maxLength := p[maxCenterIndex] - 1
// 返回最长回文
start := maxCenterIndex - p[maxCenterIndex] + 1
end := maxCenterIndex + p[maxCenterIndex]
substr := s[start:end]
return strings.Replace(substr, string(char), "", -1)
}
// 改变字符串
func changeStr(s string, char byte) string {
var new bytes.Buffer
new.WriteByte('^')
for _, b := range []byte(s) {
new.WriteByte(char)
new.WriteByte(b)
}
new.WriteByte(char)
new.WriteByte('$')
return new.String()
}
